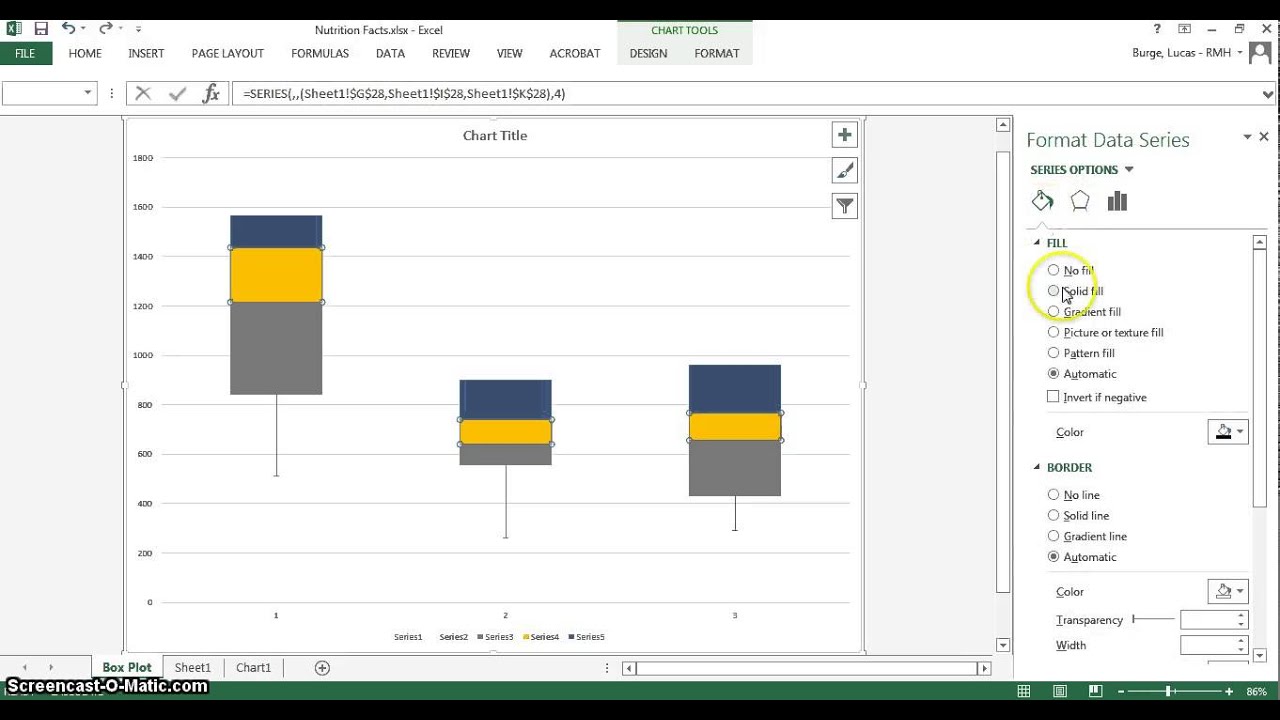
internetnoob.blogg.se - Box and whiskers plot excel 2013

Box and whiskers plot excel 2013 how to#

Waterfall Chart Creator - Create charts that compare quantity or volume to unit rates such as price/unit or profit per unit.

Sensitivity Chart Creator - Easily create sensitivity or tornado charts.

Cascade Chart Creator - Create cascade charts that help you explain your data.

Bubble Chart Creator - Quickly and easily create bubble charts from data tables.

show 1 sigma to 3 sigma bars (or none) on the statistical box and whisker plot.Ĭustomers who viewed the Box and Whisker Plot Creator also viewed:.

set whiskers for the data range or for a 1.5 sigma range.

hide or show all data points or show outliers only.

Note: you dont have to sort the data points from smallest to largest, but it will help you understand the box and whisker plot. A box and whisker plot shows the minimum value, first quartile, median, third quartile and maximum value of a data set.

Box and whiskers plot excel 2013 how to#

select multiple ranges of data from different worksheets and workbooks for the same box and whisker plot This example teaches you how to create a box and whisker plot in Excel.

create quartile, percentile or statistical box and whisker plots.

With the Box and Whisker Plot Creator, one can:: So, if one wanted to show where 90% of the points appear, one would use this versus the quartile style box and whisker plot. This is like the quartile box and whisker plot, except one can set the percentile for the gray area from 0% to 100%. One can also create a percentile box and whisker plot.

Show only outlier data points (those outside a 1.5 sigma range).

The three smaller sets of blue bars represent the 1, 2, and 3 sigma points.

The center blue bar in the second box and whisker plot is the average (as it is a statistical plot). One can set the range to be 1, 2, or 3 sigma. The gray area in this case is the 3 sigma range. The second box and whisker plot is a statistical plot. The smaller blue bars are the 1.5 sigma points. The average is plotted as a white diamond. The points outside and to the right represents the remaining 25%. The points outside of the gray to the left represents the first quartile, or 25% of the points. Again, you can verify this number by using the QUARTILE.EXC function or looking at the box and whisker plot.The first box and whisker plot above is a quartile plot The gray area is where one expects 50% of the points to be. This makes sense, the median is the average of the middle two numbers.Ħ. You can verify this number by using the QUARTILE.EXC function or looking at the box and whisker plot.ĥ. In this example, n = 8 (number of data points).Ĥ.

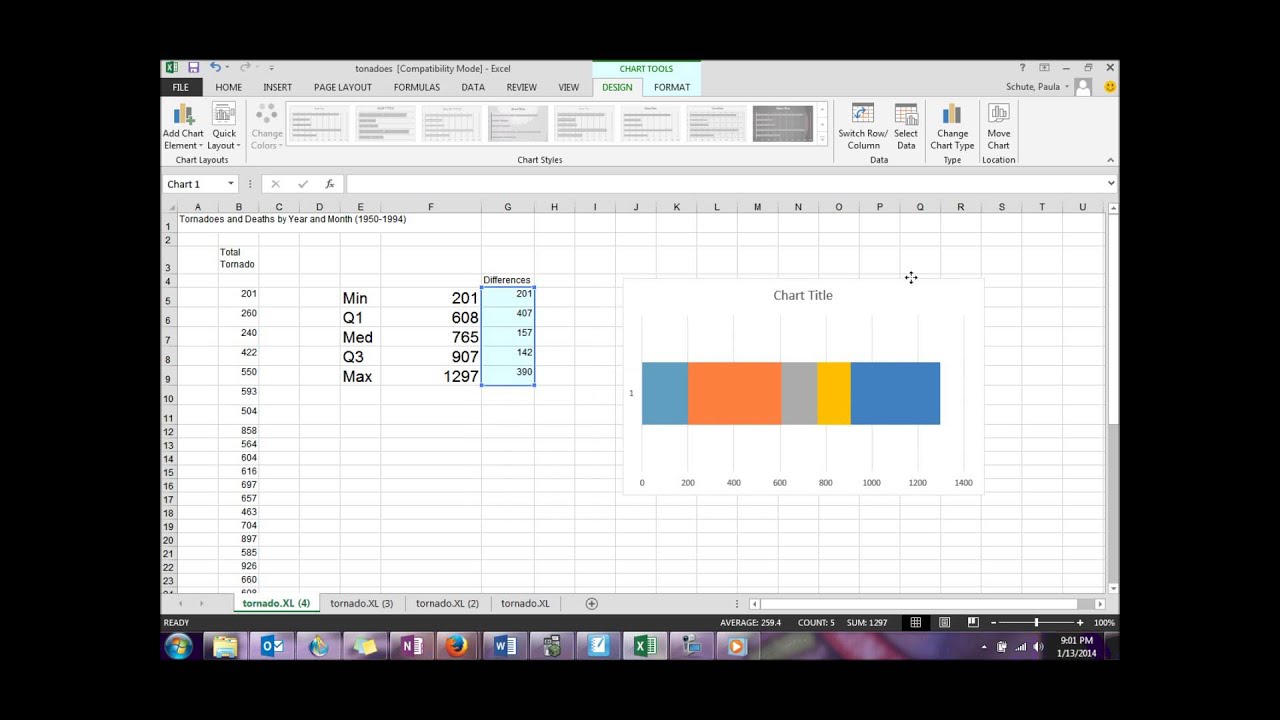
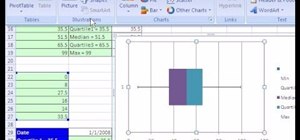
This function interpolates between two values to calculate a quartile. For example, select the even number of data points below.Įxplanation: Excel uses the QUARTILE.EXC function to calculate the 1st quartile (Q 1), 2nd quartile (Q 2 or median) and 3rd quartile (Q 3). Most of the time, you can cannot easily determine the 1st quartile and 3rd quartile without performing calculations.ġ. As a result, the whiskers extend to the minimum value (2) and maximum value (34). As a result, the top whisker extends to the largest value (18) within this range.Įxplanation: all data points are between -17.5 and 34.5. Therefore, in this example, 35 is considered an outlier. A data point is considered an outlier if it exceeds a distance of 1.5 times the IQR below the 1st quartile (Q 1 - 1.5 * IQR = 2 - 1.5 * 13 = -17.5) or 1.5 times the IQR above the 3rd quartile (Q 3 + 1.5 * IQR = 15 + 1.5 * 13 = 34.5). In this example, IQR = Q 3 - Q 1 = 15 - 2 = 13. Q 3 = 15.Įxplanation: the interquartile range (IQR) is defined as the distance between the 1st quartile and the 3rd quartile. The 3rd quartile (Q 3) is the median of the second half. The 1st quartile (Q 1) is the median of the first half. The median divides the data set into a bottom half. The x in the box represents the mean (also 8 in this example). On the Insert tab, in the Charts group, click the Statistic Chart symbol.Įxplanation: the middle line of the box represents the median or middle number (8).